SearchSpaceFactor¶
| Type: | float |
|---|---|
| Range: | [1, inf] |
| Default: | 1.0 |
| Appearance: | simple |
In a nutshell, an eigensolver approximate eigenvectors by a weighted sum over basis vectors of a lower-dimensional subspace (search space). At least the search space has a dimension of the number of sought eigenvectors (SearchSpaceFactor=1), but the larger the search space the faster is the convergence. This parameter increases the search space dimension (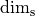 ) as follows:
) as follows:
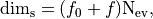
where 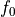 is an implementation dependent offset factor,
is an implementation dependent offset factor, 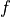 is the user defined
is the user defined SearchSpaceFactor, 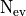 is the number of desired eigenvalues.
is the number of desired eigenvalues.