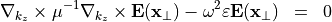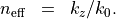PropagatingMode¶
| Type: | section |
|---|---|
| Appearance: | simple |
| Excludes: | ResonanceMode, Scattering |
This section specifies a propagating mode problem. This type of problem is also called waveguide problem.
The angular frequency 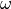 is a fixed parameter
is a fixed parameter 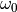 of the problem and one defines the vacuum wavelength
of the problem and one defines the vacuum wavelength 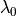 and k-vector
and k-vector 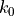 by
by
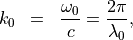
where  is the speed of light in the vacuum.
is the speed of light in the vacuum.
A waveguide geometry is characterized by a special axis, the waveguide or longitudinal direction, with a dimension much larger than the cross section diameter and measuring a huge number of wavelengths 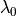 . The waveguide is then modeled as infinitely prolonged. On a macroscopic scale the waveguide axis need not to be straight.
. The waveguide is then modeled as infinitely prolonged. On a macroscopic scale the waveguide axis need not to be straight. JCMsolve can take bending effects into account, c.f., parameter AxisPositionX. Furthermore, the waveguide geometry is allowed to be twisted along the waveguide axis (parameter Twist, see also [1]).
In the following we only discuss the straight waveguide with a longitudinal axis along the  -direction. The coordinate system is chosen such that the geometry exhibits an invariance in the
-direction. The coordinate system is chosen such that the geometry exhibits an invariance in the  -direction, that is, the permittivity tensor
-direction, that is, the permittivity tensor  and the permeability tensor
and the permeability tensor 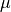 do not depend on the longitudinal direction
do not depend on the longitudinal direction  .
.
It is the aim to find propagating modes which solve Maxwell equations in source-free media and which depend harmonically on  , in the sense that
, in the sense that
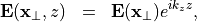
where 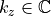 is the propagation constant and
is the propagation constant and 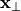 denotes the cross-section coordinates
denotes the cross-section coordinates 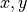 .
.
Introducing the operator
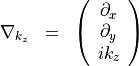
The time harmonic Maxwell’s equations of second order, see parent section, now read as
with analogue equations for the magnetic field.
The dependency on the  -coordinate has disappeared and the problem is posed on the cross-section only.
-coordinate has disappeared and the problem is posed on the cross-section only.
The above eigenmode equation has the structure of an eigenvalue problem: One seeks pairs 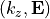 of the propagating constant and the field distribution.
of the propagating constant and the field distribution.
Traditionally, the eigenvalue is not given as the propagation constant 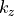 but in the form of an effective refractive index
but in the form of an effective refractive index
Bibliography
| [1] |
|