Twist¶

Type:	float
Range:	[-inf, inf]
Default:	-/-
Appearance:	optional
Excludes:	AxisPositionX, BlochVector

Specifies the twist 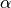$\alpha$ of a straight fiber along the waveguide axis.

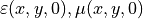The twisted fiber is not invariant in $z$ -direction. Instead, the cross-section material profiles $\varepsilon(x, y, 0), \mu(x, y, 0)$ extend into the three dimensional space by

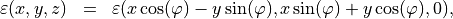
$\begin{eqnarray*} \varepsilon(x, y, z) & = & \varepsilon(x \cos(\varphi)-y \sin(\varphi), x \sin(\varphi) + y\cos(\varphi), 0), \end{eqnarray*}$

with 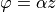$\varphi = \alpha z$ , and an analogue definition for the permeability $\mu$ .

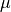In this coordinate system it is only possible to use isotropic material tensors $\varepsilon$ and $\mu$ .

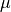This choice of helicoidal frame is consistent with the literature on twisted microstructured [1] and photonic crystal fibers [2] .

[1]	Nicolet, A., Zolla, F., Agha, Y. O., & Guenneau, S. (2007). Leaky modes in twisted microstructured optical fibers. Waves in Random and Complex Media, 17(4), 559-570.

[2]	Russell, P. S. J., Beravat, R., & Wong, G. K. L. (2017). Helically twisted photonic crystal fibres. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 375(2087), 20150440.