HeatConduction¶
| Type: | section |
|---|---|
| Appearance: | simple |
| Excludes: | ContinuumMechanics, Electromagnetics |
Heat conduction problems address the computation of the temperature distribution 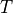 within a body. Such systems are governed by the heat equation (sometimes also called heat conduction equation):
within a body. Such systems are governed by the heat equation (sometimes also called heat conduction equation):
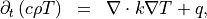
where  is the specific heat capacity,
is the specific heat capacity, 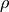 is the mass density,
is the mass density, 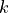 is the heat conductivity, and
is the heat conductivity, and  is a thermal source density.
is a thermal source density.
Heat convection or heat radiation within the body is not supported. On the boundaries one may impose convection-like conditions or Stefan-Boltzmann radiation conditions, c.f., boundary condition section Thermal.
The table below lists field quantities, which are implicitly defined within the solution fieldbag. This way they can be used by subsequent post-processes.
| Quantity | Expression | JCM Tag |
|---|---|---|
| thermal flux density | 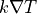 |
ThermalFluxDensity |
| thermal energy density | 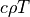 |
ThermalEnergy |