MultipoleExpansion¶

Type:	section
Appearance:	simple
Excludes:	CartesianToFourierTransform, ConvertToPowerFlux, CreateReducedBasis, DensityIntegration, DipoleEmission, EvaluateReducedBasis, ExportFields, ExportGrid, FarField, FluxIntegration, FourierTransform, GridStatistics, IntegrationWeights, LayeredMediaSolver, ModeOverlap, OpticalImaging, PupilField, Radiation, ResonanceExpansion, ResonanceOverlap, ScatteringMatrix, Superposition, SurfaceDensityIntegration

Use this post-process to obtain the multipole expansion of a time-harmonic electromagnetic field in a lossless homogeneous isotropic exterior.

In a nutshell, the outgoing electromagnetic field is determined and decomposed into contributions from various spherical vector waves or multipoles. These radiate radially outwards, thus fulfilling the Sommerfeld radiation conditions, and travel towards infinity.

Example: A multipole expansion post-process may be specified as follows:

PostProcess {
  MultipoleExpansion {
    FieldBagPath = "./project_results/fieldbag.jcm"
    OutputFileName = "./project_results/expansion_coefficients.jcm"
    Format = JCM-ASCII
    MultipoleDegree = 2
  }
}

Theoretical background

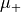It is required that the scatterer is surrounded by a lossless, homogeneous and isotropic material distribution enclosing the origin. Let $\varepsilon_+$ and $\mu_+$ denote the corresponding scalar permittivity and permeability, respectively. The angular wave number is given by 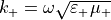$k_+=\omega \sqrt{\varepsilon_+ \mu_+}$ . 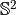In this setting, the scattered electromagnetic field at a point $\pvec{r}$ can be expanded into a basis of vector spherical wave functions which are orthonormal on the unit sphere $\mathbb{S}^2$ .

$\begin{eqnarray*} \VField{E}_{sc}(\pvec{r},k_+) = \sum_{n=1}^{\infty} \sum_{m=-n}^n \left[ a_{nm}\pvec{N}_{nm}(\pvec{r},k_+) + b_{nm}\pvec{M}_{nm}(\pvec{r},k_+ )\right]. \end{eqnarray*}$

The coefficients 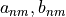$a_{nm},b_{nm}$ are determined by the following integrals

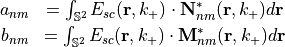
$\begin{eqnarray*} a_{nm} & = \int_{\mathbb{S}^2} E_{sc}(\pvec{r},k_+)\cdot\pvec{N}_{nm}^\ast(\pvec{r},k_+) d\pvec{r} \\ b_{nm} & = \int_{\mathbb{S}^2} E_{sc}(\pvec{r},k_+)\cdot \pvec{M}_{nm}^\ast(\pvec{r},k_+) d\pvec{r} \end{eqnarray*}$

The vector spherical wave functions 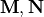$\pvec{M},\pvec{N}$ for the outgoing fields have the following definition in terms of spherical coordinates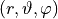 $(r,\vartheta,\varphi)$

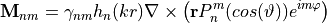
$\begin{eqnarray*} \pvec{M}_{nm} = \gamma_{nm} h_{n}(kr)\nabla\times\left(\pvec{r} P_{n}^m(cos(\vartheta))e^{im\varphi}\right) \end{eqnarray*}$

$\begin{eqnarray*} \pvec{N}_{nm} = \frac{1}{k} \nabla \times \pvec{M}_{nm} = \gamma_{nm} \left[ \frac{n(n+1)}{kr}h_{n}(kr) \frac{\pvec{r}}{r} P_{n}^m(cos(\vartheta))e^{im\varphi} + \frac{r}{kr} \frac{d}{d(kr)}\left(kr h_n(kr)\right) \nabla \left( P_{n}^m(cos(\vartheta))e^{im\varphi} \right) \right] \end{eqnarray*} with the common normalization factor$

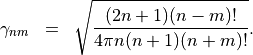
$\begin{eqnarray*} \gamma_{nm} & = & \sqrt{\frac{(2n+1)(n-m)!}{4\pi n (n+1)(n+m)!}}. \end{eqnarray*}$

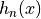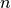The definition makes use of the spherical Hankel functions of the first kind $h_n(x)$ and the associated Legendre polynomials $P_n^m(x)$ of degree $n$ and order $m$ .

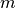Storage format

The computed multipole expansion is stored in a JCM table. Each row in the table corresponds to a vector spherical wave function. Summing up (superimposing) these spherical waves gives an approximation of the scattered field:

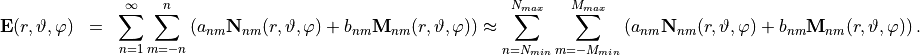
$\begin{eqnarray*} \VField{E}(r, \vartheta, \varphi) & = & \sum_{n=1}^{\infty} \sum_{m=-n}^n \left( a_{nm}\pvec{N}_{nm}(r,\vartheta, \varphi) + b_{nm}\pvec{M}_{nm}(r,\vartheta, \varphi) \right) \approx\sum_{n=N_{min}}^{N_{max}} \sum_{m=-M_{min}}^{M_{max}} \left( a_{nm}\pvec{N}_{nm}(r,\vartheta, \varphi) + b_{nm}\pvec{M}_{nm}(r,\vartheta, \varphi) \right) . \end{eqnarray*}$

The type (electric or magnetic multipole moments) is stored on the first columns as a binary variable. The output JCM table file has the following columns:

Columns 1: Type

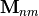This is type of the vector spherical wave function $\pvec{N}_{nm}$ or $\pvec{M}_{nm}$ (as explained above) encoded in a binary variable: 1 indicates 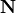$\pvec{N}$ type and a 0 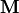$\pvec{M}$ type.
Columns 2-3: n, m

The second and third columns contain the integer multipole degree n and order m of the vector spherical wave function $\pvec{N}_{nm}$ .
Columns …: ExpansionCoefficient_<iF>, …

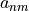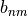The subsequent columns contain the expansion coefficients $a_{nm}$ or $b_{nm}$ of the respective vector spherical wave function. The index <iF> stands for the field index.