Function¶
| Type: | string |
|---|---|
| Range: | [] |
| Default: | -/- |
| Appearance: | simple |
| Excludes: | Expression |
| Requires: | Module |
Used in combination with Module to specify the python function containing the “relative permittivity”- tensor field definition.
In the most simple case a Python module is a .py-file which contains one or several python function definition. In this case the name of the module is simply the file name without its .py suffix. The parameter Function is used to pick out the desired function.
The so specified Python function must return a Python tuple or, preferable, a NumPy array of the appropriate shape (relative permittivity is a 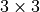 - matrix) and must accept a single argument which is a dictionary containing the parameters as defined by the Parameter sections:
- matrix) and must accept a single argument which is a dictionary containing the parameters as defined by the Parameter sections:
# import numpy package
from numpy import *
def your_function_name(parameter):
x = parameter['X'] # retrieving the position
# add your code here
return value # returns a :math:`3 \times 3` - matrix
Note
The position 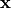 and the time
and the time  are implicitly inserted into the parameter dictionary with keys
are implicitly inserted into the parameter dictionary with keys X and t respectively. For time-harmonic electromagnetic problems the angular frequency 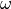 is inserted with key
is inserted with key EMOmega, if uniquely defined (EM stands for “electromagnetic”).
In a first practical example we want to give the 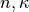 based definition of the relative permittivity, where
based definition of the relative permittivity, where 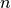 denotes the refractive index and
denotes the refractive index and  the extinction factor. We want to assume that the relative permittivity is
the extinction factor. We want to assume that the relative permittivity is 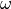 dependent in the following sense:
dependent in the following sense:
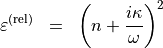
Assuming that the respective Python implementation is contained in module PythonTensorFieldLibrary with function name NK_Permittivity, the JCM-syntax looks like this:
RelPermittivity {
Python {
Module = "PythonTensorFieldLibrary"
Function = "NK_Permittivity"
Parameter {
Name = "nk"
VectorValue = [..., ...] # set n,k here
}
}
}
Tip
It is easier to define this simple example as an inline Python expression as shown in Expression.
The used Python function may have the following form:
from numpy import *
def NK_Permittivity(parameter):
n = parameter['nk'][0] # retrieving n
k = parameter['nk'][1] # retrieving k
w = parameter['EMOmega'] # retrieving omega
return pow(nk[0]+1j*nk[1]/w), 2)*eye(3, 3)
As a second example we want to define a relative permittivity which varies with the temperature:
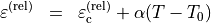
The first term is a constant value. The second term is a thermo-optical correction. This correction term has one field parameter - the temperature - and two coefficient parameters, the thermo-optical coefficient 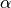 and a standard temperature value
and a standard temperature value 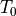 .
.
Assuming that the respective Python implementation is contained in modulePythonTensorFieldLibrarywith function nameThermoOpticalCorrection, the JCM-syntax looks like this:
RelPermittivity {
Constant = ... # set first term eps_c, here
Python {
Module = "PythonTensorFieldLibrary"
Function = "ThermoOpticalCorrection"
Parameter {
Name = "T"
FieldValue {
FieldBagPath = ... # path to a temperature field
Quantity = Temperature
}
}
Parameter {
Name = "a"
VectorValue = ... # scalar thermo-optical coefficient
}
Parameter {
Name = "T0"
VectorValue = ... # standard temperature
}
}
}
Tip
It is easier to define this simple example as an inline Python
expression as shown in Expression.
The used Python function may have the following form:
from numpy import * def ThermoOpticalCorrection(parameter): T0 = parameter['T0'] # retrieving T0 a = parameter['a'] # retrieving a w = parameter['EMOmega'] # retrieving omega return a*eye(3, 3)*(T-T0)