MirrorSymmetry¶
| Type: | Vector<enum> |
|---|---|
| Range: | [v_1, …], v=ElectricSymmetric|MagneticSymmetric |
| Default: | -/- |
| Appearance: | optional |
In the presence of mirror symmetries it is required to specify the field behavior of the symmetric resonance mode across any mirror planes. A mirror plane is characterized by its normal vector  . For type
. For type ElectricSymmetric the electric field is polarized within the mirror plane and the magnetic field is perpendicular to the mirror plane:
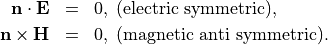
For type MagneticSymmetric we have
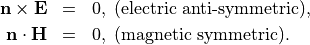
For multiple mirror planes you must specify all individual mirror symmetry types in a vector. Thereby, the mirror planes (maximum two planes) are ordered by the following convention: A mirror plane with normal  comes before another mirror plane with normal
comes before another mirror plane with normal 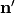
 , or
, or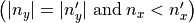
Note
The mirror planes together with their normals and ordering are shown within JCMsuite.