Stratification¶

Type:	section
Appearance:	optional

This section is used to define a stratified blank / substrate. As shown in Figure “Stratified blank”, the blank is equipped with coordinates 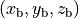$(x_\mathrm{b}, y_\mathrm{b}, z_\mathrm{b})$ . The stratification is normal to the 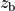$z_\mathrm{b}$ direction which coincides with the optical axis when the blank is not tilted (as set by the parameter Rotation).

Stratified blank¶

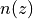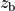The refractive index $n(z)$ is a piece-wise constant function of $z_\mathrm{b}$ ,

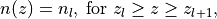
$\begin{eqnarray*} n(z) = n_l, \; \mbox{for}\; z_{l} \geq z \geq z_{l+1}, \end{eqnarray*}$

where 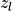$z_l$ is the position of the 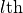$l\mbox{th}$ interface. 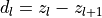$d_l=z_{l}-z_{l+1}$ denotes the thickness of the 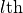$l\mbox{th}$ layer. The medium above the blank ( 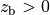$z_\mathrm{b}>0$ ) has the refractive index 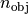$n_{\mathrm{obj}}$ of the optical system’s object space whose value is taken from the input Fourier transform data InputFileName. 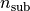The multilayer stack is followed by an infinite thick substrate of refractive index $n_\mathrm{sub}$ .

In case of a transmissive blank, the substrate refractive index 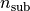$n_\mathrm{sub}$ is taken from the input file InputFileName as well. This is possible since a Fourier transform file contains information on the illumination. For transmissive blanks the substrate is the half space from which the scatterer is actually illuminated.

For a reflective optical system, the user must specify 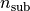$n_\mathrm{sub}$ .